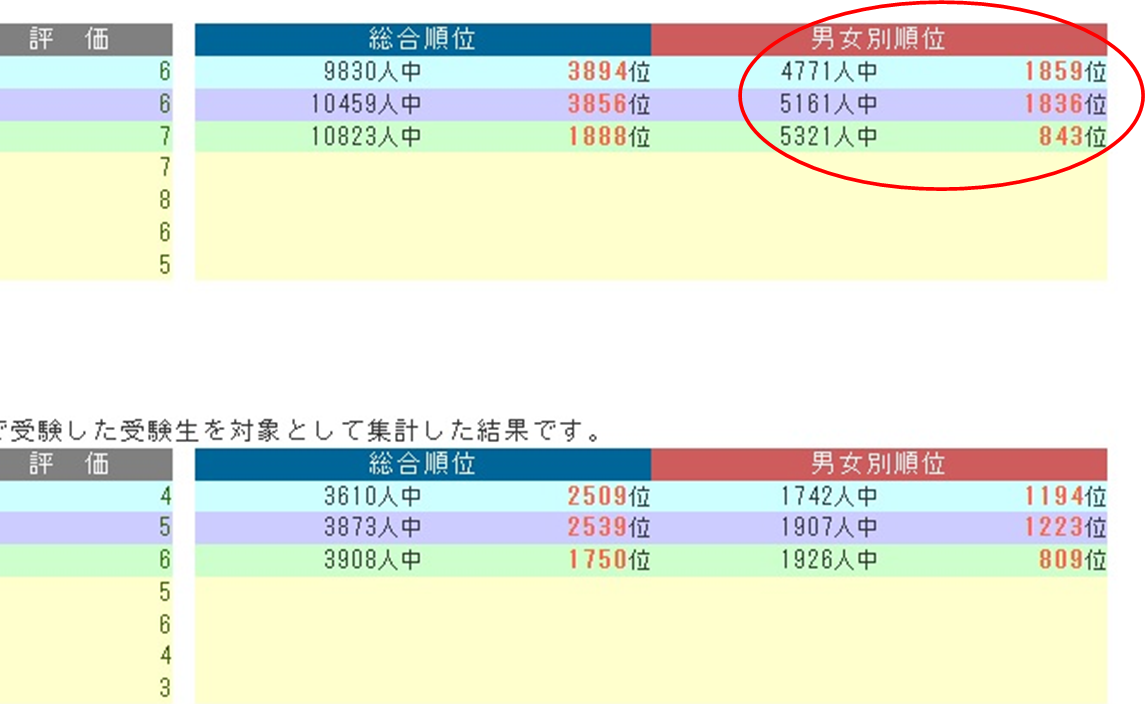
日能研に通うと毎週のように「育成テスト」がある。その結果について評価でなく順位を偏差値に換算して今の立ち位置を確認するようにしていた。
評価が10段階で表示されるがイマイチどんなもんだかわからない
育成テストの結果では、点数と平均点と順位と評価が提示される。受験界隈みんな大好きな偏差値は提示されない。ここので唯一成績っぽく示される評価について一般的に言われていることは、以下のような感じである。
上位層だと、評価「６」：偏差値50-54、「７」：偏差値55-59、「８」：偏差値60-64、「９」：偏差値65-69、「１０」：偏差値70以上
逆に下位層だと、評価「５」：偏差値45-49、評価「４」：偏差値40-44、評価「３」：偏差値35-39、評価「２」：偏差値30-34、「１」：偏差値29以下
となる。
評価「１１」や「０」があるのかはわからない（たぶんない）。しかし、おわかりだと思うが、同じ評価「７」でも偏差値55と偏差値59では気分も立ち位置もだいぶ違う。
そこで評価でなく順位から偏差値を割り出す
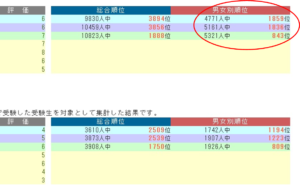
こちらはさきほどの育成テストの成績表。一番上の行で、男女別順位は4科目合計で4771人中/1859位である。
ここで、順位を全体の人数で割ってみる。
1859÷4771=0.389・・
つまり上から38.9%ぐらいの位置にいることがわかる。
ここでこの成績分布をとりあえず正規分布と仮定してみる。
↑のサイトに偏差値と上位パーセントの比率が出ているのでこれを参考にすると・・・
偏差値と上位パーセント・割合の表
| 偏差値 | 上位% | 何人に一人? |
| 80 | 0.13% | 740.8 |
| 79 | 0.19% | 536.0 |
| 78 | 0.26% | 391.4 |
| 77 | 0.35% | 288.4 |
| 76 | 0.47% | 214.5 |
| 75 | 0.62% | 161.0 |
| 74 | 0.82% | 122.0 |
| 73 | 1.07% | 93.2 |
| 72 | 1.39% | 71.9 |
| 71 | 1.79% | 56.0 |
| 70 | 2.28% | 44.0 |
| 69 | 2.87% | 34.8 |
| 68 | 3.59% | 27.8 |
| 67 | 4.46% | 22.4 |
| 66 | 5.48% | 18.2 |
| 65 | 6.68% | 15.0 |
| 64 | 8.08% | 12.4 |
| 63 | 9.68% | 10.3 |
| 62 | 11.51% | 8.7 |
| 61 | 13.57% | 7.4 |
| 60 | 15.87% | 6.3 |
| 59 | 18.41% | 5.4 |
| 58 | 21.19% | 4.7 |
| 57 | 24.20% | 4.1 |
| 56 | 27.43% | 3.6 |
| 55 | 30.85% | 3.2 |
| 54 | 34.46% | 2.9 |
| 53 | 38.21% | 2.6 |
| 52 | 42.07% | 2.4 |
| 51 | 46.02% | 2.2 |
| 50 | 50.00% | 2.0 |
上位38.9%は偏差値52(上位42.07%)と偏差値53(上位38.21%)の間に位置していることがわかる。
つまり、上位38.9%は偏差値52の後半くらいだということがわかる。
実際の評価も「６」：偏差値50-54なので、だいたいあっていることがわかる。
同じように国語算数の2科目でやってみる。
843位/5321人中なので、
843÷5321=0.1584・・・
全体の15.84%ぐらいの位置。
さきほどの正規分布を見ると偏差値60(上位15.87%)と偏差値61(上位13.57%)の間なので、偏差値60をわずかだけ上回ったということがわかる。評価は「７」だったが、限りなく「８」に近い「７」だったいうことがわかる。
毎回の順位を偏差値に換算して立ち位置を見た
試験の度に↑のように順位を偏差値に換算して、その推移をエクセルの表にしてみた。仕事では面倒なのでエクセルとか使って資料とか作らないわけなのだが、こういう時は威力を発揮する笑。
こうすることで、５とか６とか７とか1段階のメリハリがない評価よりも、偏差値というわかりやすい物差しでより立体的になった。
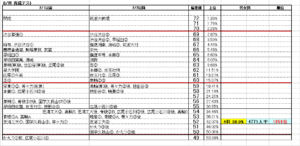
そして、このように、偏差値と各中学校のR4偏差値（合格ライン80％の偏差値）を合わせて表にすると、より自分の立ち位置が明確になった。エクセル様様である。
毎回テストの度にこの表を印刷して、テストの成績と中学校の偏差値を結び付け、子供に自分がどのレベルにいるのかを意識させた（が、子供が本当に意識していたかは不明）。
これをやってると見えてくる不明なポイント
Q 男女別の順位で計算したが、男女全体の順位でやるべきでは？
A 受験する想定の中学校が男子校がメインだったため男女別で計算した。共学メインなら男女合計がよいかもしれない。しかし、実際にはほぼ誤差の範囲。さきほどの育成テストでは男女別は38.9%であったが、合計順位3894位/9830人中で計算しても39.6%と１％以内の誤差だった。ただし、男子が得意の算数理科、女子が得意の国語社会なのが一般的なので、そのバランスが取れているのが前提。算国理のように男子得意よりの３教科は注意だ。
Q 受験種別で問題がかわるがどうするか。上位のクラスでの順位をどう判断するか
A さきほどの育成テストの実例であれば、
基本集計 1859位/4771人中 上位38.9%
受験種別 1194位/1742人中 上位68.5％
となる。この場合は、上の基本集計の順位1859位で判断する。
しかし、以下のテストの時は、
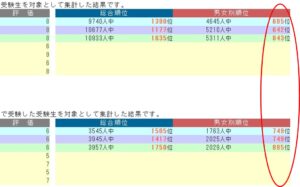
基本集計 695位/4645人中 上位14.9%
受験種別 749位/1763人中 上位42.4％
この場合は、749位を全体の4645人で割って、749÷4645=0.161・・
下側の上位16.1％を偏差値の根拠とした。
基本的には悪い方の順位で計算すべきだと思う。ただ、基本問題は間違えまくったけど、受験種別の方の問題は正解しまくった場合などはそちらの成績で判断してもよいかと思う。その辺の判断基準は難しくて、受験が終わった今でもどっちにすべきかの基準はよくわからない。
Q 全国公開模試と育成テストの関係性は
A そもそも育成テストと全国公開模試を同じように偏差値で見ていいのかという問題がある。最初に提示した育成テストの母集団は男女別4771人/男女合計9830人。その1週間後に開催された全国公開模試の受験人数は男女別4777人/男女合計9809人と育成テストと数人単位しか母数はかわらなかった。なので、育成テストの受験人数を偏差値の根拠としても十分良いと思われる。
ということで、このエクセル化はぜひやってほしいですねと笑。
